The data provided in these reports are typically presented as they were recorded – the only processing has been to convert the data to engineering prototype units and to attach some zero reference to each time history.
Some signal processing will generally be necessary, especially for integrating accelerometer records. The most appropriate choice of filtering techniques is dependent on the characteristics of the instruments, amplifiers, and data acquisition system.
Integrating accelerometer time histories without proper filtering will produce drift in the calculated velocities and displacements. The following information was taken from Wilson 1998 and from Wilson et al. 1998. If there are any questions regarding the format of the data or in interpreting and processing the data presented on these web pages, please contact the Center at cgm@ucdavis.edu.
For additional reading on FFT’s and digital signal processing, I’ve found the following to contain useful information:
FFTW offers free C subroutines for calculating discrete Fourier Transforms. They also maintain a list of useful web sites dealing with the FFT and its applications.
Brigham, E.O. (1988) The Fast Fourier Transform and its Applications, Prentice Hall Signal Processing Series, ISBN 0-13-307505-2
Development of Signal Processing Procedures
Signal processing and integration methods were developed for calculating displacement time histories from acceleration time histories. The development of a reliable procedure for double-integration of accelerometers was necessary to: (1) evaluate the deformed shape of the free-field soil profile, which forms an essential input to several of the analysis methods presented later in this dissertation; and (2) evaluate aspects of the modeling system such as container effects, container rocking, and uniformity of motions.
Displacements tend to be dominated by low frequencies, but the accelerometers used in this study, like most piezoelectric accelerometers, are not capable of recording very low frequencies. High-pass filters are generally included in the analog circuits to prevent drift in piezoelectric accelerometer signals. Analog high-pass filters remove low frequency information, but also corrupt the amplitude and phase of the signal near the filter corner frequency. To remove the corrupted acceleration data, non-causal digital high-pass filters were applied in the frequency domain using a 10th order zero phase delay Butterworth filter.
Maximizing the useful amount of low frequency data from the acceleration records is somewhat subjective, requiring careful consideration of signal processing techniques, the instrumentation characteristics, the signal conditioning and data acquisition systems, and the characteristics of the physical system being studied. There are over 1400 acceleration time histories in the suite of tests reported in this dissertation, so looking at each record individually was not deemed reasonable. Fortunately, the noise characteristics are generally similar in all acceleration time histories because they all (with few exceptions) come from the same accelerometer type and pass through the same electronic components before being recorded. Thus, a single high-pass corner frequency was selected for mass-processing of all the acceleration time histories. Selection of the optimum high-pass corner frequency was based on detailed analyses of representative recordings, and the following considerations.
The input base motions had been high-pass filtered at about 0.3 Hz to reduce the peak displacements to values that the shaker could physical accommodate. Consequently, there is little input motion below this frequency from the shaker.
Fourier spectra of acceleration time histories almost always had a sharp decay in spectral amplitude at about 0.1 Hz, and the spectral amplitude progressively increased below that frequency (a common characteristic of accelerometer noise; as illustrated in Figure 3.24). Integration of the acceleration time histories resulted in calculated displacements that were dominated by very large, low frequency drifts unless the spectral content below about 0.1 Hz was filtered out.
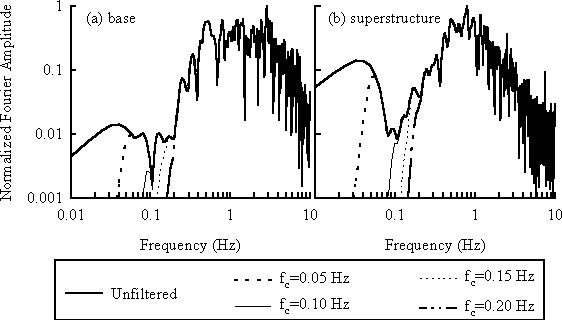
High-pass filtering with a 10th order Butterworth filter applied only to the spectral magnitudes (acausal filter) was found to yield better displacements than those calculated using lower order Butterworth filters (e.g., a 4th order filter is common). This relatively steep filter appears to work best because the acceleration spectra also have steep drop-offs with narrow windows of frequencies over which the spectral amplitudes are very small. This is evident in the accelerometer spectra presented in Figure 1, where the unfiltered spectra from two locations in one event are shown with various filtered spectra.
Figure 1: Fourier spectra of accelerations in Csp2 event F filtered with 10th order IIR Butterworth filters
Several instrumentation tests were performed where pairs of accelerometers were placed on opposite ends of a linear potentiometer that was measuring the relative displacement between two objects on the centrifuge. Integration of the accelerometers gives absolute displacements, and thus the relative displacement could be obtained by subtracting the two integrated time histories. The relative displacement time histories recorded by the linear potentiometers were compared to those obtained by double-integrating the accelerometers. The best average agreement between the potentiometers and accelerometers was obtained using a corner frequency of about 0.15 Hz.
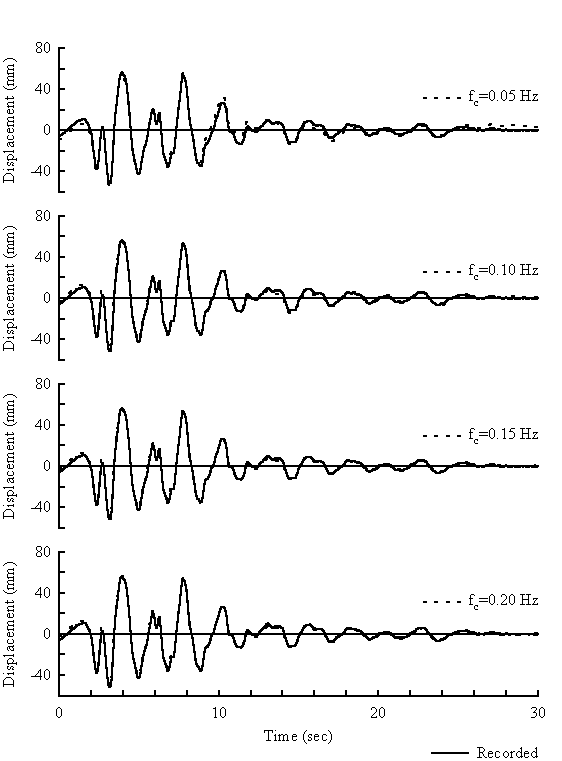
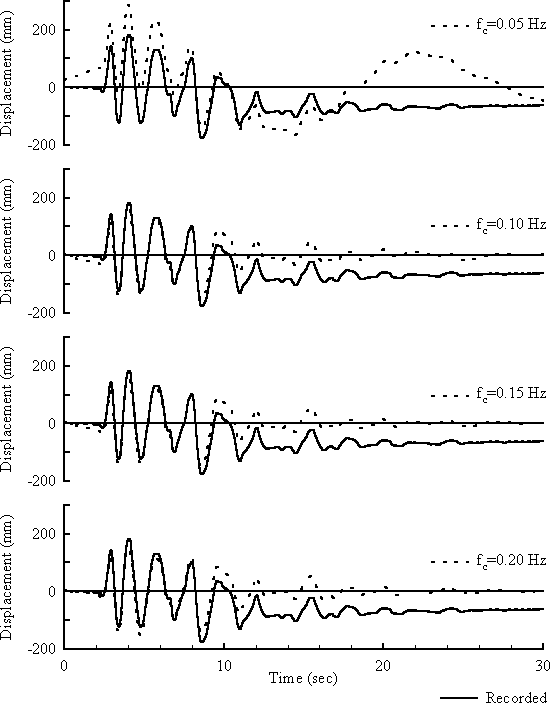
Figures 2 and 3 show comparisons of displacement time histories obtained by integrating acceleration time histories together with those recorded by linear potentiometers. Both figures show results for the range of corner frequencies shown in Figure 1. Figure 2 is for a case where no permanent deformations occurred, and illustrates the very good agreement obtained in such cases. The displacements change very little as the filter corner is changed, as there is very little low frequency content in the signal [see Figure 1(a)]. Figure 3 is for a case with significant permanent deformations, and illustrates how the accelerometers captured the transient deformations but not the permanent deformations. From Figure 1(b), we can see there is more low frequency signal in this record, so the choice of filter corner has more effect on the calculated displacements. Note, however, that as more low frequency signal is included, the calculated displacements do not approach the recorded values.
Figure 2: Effect of changing corner frequency on calculated displacement of the base relative to the manifold – Csp2 event F
Figure 3: Effect of changing corner frequency on calculated displacement of the superstructure relative to the top ring – Csp2 event F
Numerous comparisons such as shown in this figure provided an appreciation of this limitation on displacements obtained by integrating accelerometers. Attempts to calculate the relative displacements from acceleration records with too little digital high-pass filtering produce obvious drift and poor approximations to the recorded displacement. Increased filtering of the data results in a good approximation to the dynamic component of displacement, but the permanent component is lost. Any real signal related to permanent displacement is obscured by noise, and thus removed by the high-pass filtering.
Note detailed examination of individual records is needed for certain analyses, including the work assembled in Wilson (1998). For example, while the earlier specified corner of 0.15 Hz yielded the best results on average (i.e. best match to recorded displacements when available), the back-calculation of p-y curves in Chapter 5 required all the accelerometers in a particular event to yield reasonable displacements. For these calculations the filter corner was raised to 0.25 Hz. This eliminated the corrupted low frequency data from virtually all the accelerometers. While some real data was unavoidably removed, the trends in behavior are adequately captured.
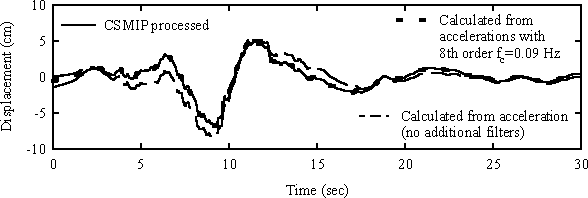
Neither the method of integration nor the type of filter are critical factors in calculating displacements, as long as the filters have similar characteristics (i.e. corner frequency, phase, and slope). For example, consider the acceleration and displacement data for the UCSC/LICK LAB (ch. 1-90 deg.) site during the Loma Prieta earthquake as provided by the California Strong Motion Instrumentation Program, CSMIP. The Volume II displacements given by CSMIP were calculated using the Caltech method and are plotted in Figure 4. In the Caltech method (Hudson 1979) for processing ground motion accelerograms, a 250 point smoothing window (Ormsby filter) is typically applied in the time domain and the record is double integrated using the trapezoidal rule. The filter is then applied again to the velocity, and again to the displacements. As seen in Figure 4, the CSMIP displacements agree well with displacements calculated by taking the Fast Fourier Transform (FFT) of the volume II accelerations (Ormsby filter has been applied once), applying a non-causal Butterworth filter only to the magnitude (not to the phase) of the acceleration spectrum, dividing the filtered spectrum by -(omega)2, and taking the inverse FFT. Note that double integration in the time domain transforms to division by -(omega)2 in the frequency domain. An 8th order Butterworth filter with a high pass corner frequency of 0.09 Hz was used to approximate the Ormsby filter used by CSMIP, which ideally removed all frequency content below 0.05 Hz, passed all frequency content above 0.1 Hz, and scaled the magnitude of the frequency content linearly between these two frequencies. The displacements calculated using either method are virtually identical except near the beginning and end of the record (the end is not shown), where the maximum errors due to effects of digital filtering are expected (see Hudson 1979). Figure 4 also shows displacements calculated without filtering the volume II accelerations, showing that the filters have a significant effect on calculated displacements. Note the volume II accelerations published by CSMIP have been filtered, but double integrating these accelerations will not result in the volume II displacements because the implementation of the Ormsby filter passes some low frequency content. Thus the need to filter the velocities and displacements calculated using the Caltech method.
Figure 4: Reported versus calculated displacements from Loma Prieta earthquake
References:
Hudson, D.E. 1979. Reading and Interpreting Strong Motion Accelerograms. EERI Engineering Monographs on Earthquake Criteria, Structural Design, and Strong Motion Records, Vol. 1.
Wilson, D.W., Boulanger, R.W., and Kutter, B.L. (1998). “Signal processing for and analyses of dynamic soil-pile interaction experiments,” Proceedings, Centrifuge 98. Kumura, Kusakabe, and Takemura, Eds. Balkema, Rotterdam, pp. 135-140.
Wilson, D.W. (1998). “Soil-pile-superstructure interaction in liquefying sand and soft clay.” Ph.D. Dissertation, UCD/CGM-98/04